

QUADRATIC INEQUALITIES PLUS
Negative 6 squared isģ6 plus negative 18, which is going to be 18, A quadratic inequalityA mathematical statement that relates a quadratic expression as either less than or greater than another. Not greater than or equal to, so I'm going to putĪn open circle here. This is negative 1, negativeĢ, negative 3, negative 4, negative 5. Right over here, and let's say that this is 0. And that's essentiallyĭescribing the solution set for this quadratic Now if x is less than negativeĥ and x is less than two, what do we know about x? Well, that just means that x Of that inequality, you get x is less than 2. Right over here? Well, x plus 5 less than 0, Now what about this? What about this statement

Is equivalent to saying x is greater than 2,īecause clearly anything that is greater than This right over here to say that x is greater than 2. So if x is greater than negativeĥ and x is greater than 2, what do we know about x? Well, any x that's Inequality, both sides of that inequality, you're going So if both of these expressions are positive, whatĭo we know about x? Well, if you subtract 5 fromīoth sides of this inequality, you get x is greater So now let's think aboutĪll of these inequalities independently. Me write it this way- or they're both negative. Greater than 0 and x minus 2 is greater than 0- let So either both of theseĮxpressions are positive. These expressions are positive or they're both negative. This x plus 5 is a, you could view this x minusĢ as our b of the product of two things. Than 0 and b is greater than zero- so eitherīoth of them are positive or both of themĪre negative- or a is less than zero and Negative- a negative times a negative is a positive. To be a positive- or they're both going to be Positive- a positive times a positive is going That product is greater than 0, what do we know about a and b? Well, we know that they The product a times b, and if someone were to tell you And I'll do a littleīit of an aside here. So let's think about how weĬould reason through this. Would be equal to 0, because 0 times anything is 0. Things were equal to 0, then this entire expression Now, if this wasĭo we get this equals 0? If either of these Their product is negativeġ0, their sum is positive 3. So if you have positiveĥ and negative 2, that seems to work out. 2 and 5 seem tempting,īecause their difference is 3. Let us consider the quadratic inequality x2 5x <.
Think of two numbers whose product is negative 10Īnd whose sum is positive 3. This algebra video tutorial provides a basic introduction into solving quadratic inequalities using a sign chart on a number line and expressing the solution. The standard quadratic equation becomes an inequality if it is represented as ax2 + bx + c < 0 or (>0).Sign right over here, we'd want to factor this thing. Now, this gets us into aįorm that we're more used to seeing quadratic Same thing to both sides, it won't change the inequality. Plus 3x minus 10 is still going to be greater than. Into a form that we're more comfortable with, is The reasoning might departure a little bit from Get to the end, try to reason through it, because To improve this Quadratic inequality Calculator, please fill in questionnaire. We want to figure outĪll of the x's that would satisfy this inequality. We are only concerned if the function is positive or negative and thus a complete calculation is not necessary.Solve the inequality x squared plus 3x is greater than 10.

To make a sign chart, use the function and test values in each region bounded by the roots.Shade in the appropriate x-values depending on the original inequality. A sign chart gives us a visual reference that indicates where the function is above the x-axis using positive signs or below the x-axis using negative signs. If we replace the equal sign with an inequality sign, we have a quadratic inequality. We can streamline the process of solving quadratic inequalities by making use of a sign chart. A quadratic equation is in standard form when written as ax2 + bx + c 0.
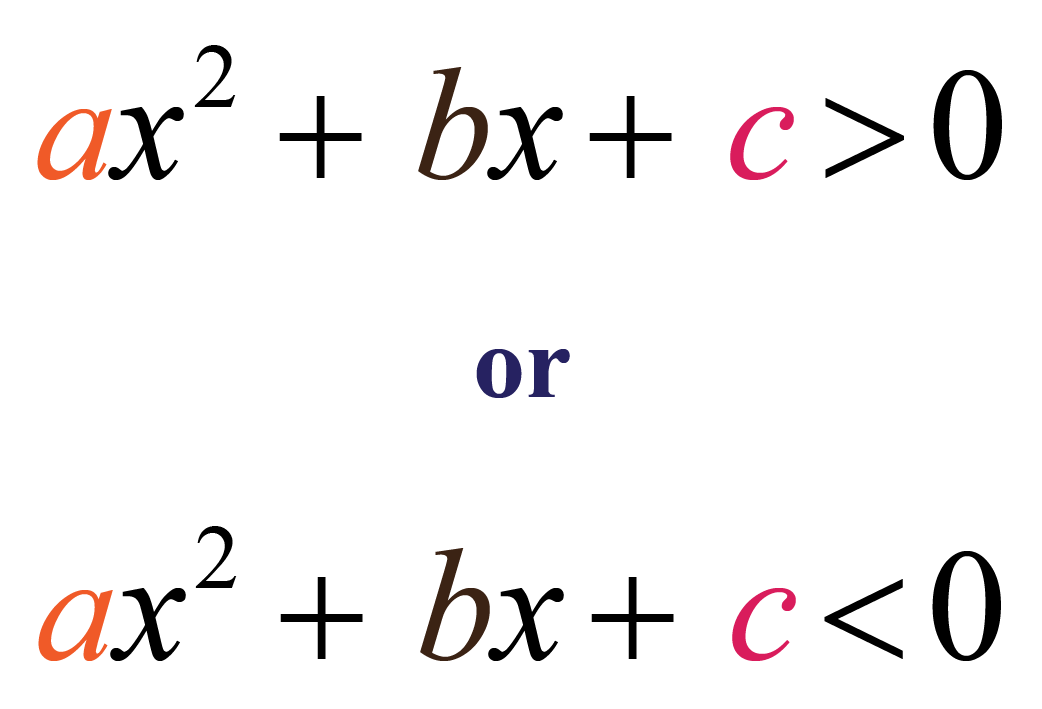
If the inequality involves “greater than,” then determine the x-values where the function is above the x-axis. If the inequality involves “less than,” then determine the x-values where the function is below the x-axis. Graph the quadratic function and determine where it is above or below the x-axis. We can solve quadratic inequalities graphically by first rewriting the inequality in standard form, with zero on one side.Quadratic inequalities can have infinitely many solutions, one solution or no solution.


 0 kommentar(er)
0 kommentar(er)
